超声概念与通识

一、超声概念与声学方程

1.1 超声成像原理

我们不去讲那些简单易懂的回波理论，这些都是较为常识的内容，这里讲的是如何从数学上剖析超声成像

目前我还没找到声学方程到底在超声成像研究有啥用，等悟了以后再补充

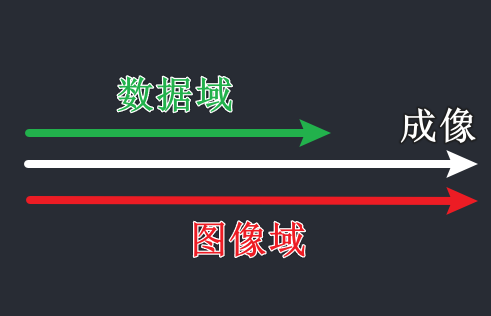
超声成像可以从两个角度来理解，这两个角度对应着两个不同的模型，他们之间彼此不同，但又有着递进关系。

第一个模型叫做图像域模型： $g= f * \text{PSF}$ 。关注的是成像系统成出来的那个“像素点”长什么样

第二个模型叫做数据域模型： $Sx=P$ 。关注的是“探头在数据层看到的是什么”

上来就这么说有些令人费解，接下来会先分别讲述从这两个不同角度出发的超声成像，然后最后再来看看他们的联系，还有为什么有着递进关系。

1.1.1 从PSF（图像域）来看

超声成像过程可以很好地用*点扩散函数（Point Spread Function, PSF）*与卷积模型来描述。通过从一维、二维到三维的推导，可以清晰理解超声图像是如何由真实散射体分布*与系统特性*共同决定的。

时域中的卷积=频域中的乘积或内积

1.1.1.1 一维：两个散射点的成像

假设在深度方向（z 轴）上有两个点散射体 $f$ ，位置分别为 $z_1$ 、 $z_2$ ，反射系数分别为 $a_1$ 、 $a_2$ ，真实的散射分布为：

f(z) = a_1 \,\delta(z - z_1) + a_2 \,\delta(z - z_2)

系统的轴向（时域、或者说竖着的）点扩散函数记为 $h(z)$ ，表示系统对一个点目标的回波响应（即脉冲包络）。

成像结果 $g(z)$ 是真实分布和 PSF 的卷积：

g(z) = f(z) * h(z) = a_1 \, h(z - z_1) + a_2 \, h(z - z_2)

每个点的成像结果都是一个波包，多个点的成像是这些波包的叠加。如果点间距小于 PSF 的 FWHM，会出现波包重叠、难以分辨；点间距足够大，则可以分开。

如果要求 $f$ ，那就需要对 $g$ 进行反卷积，卷积核就是PSF。

1.1.1.2 二维：一个平面散射分布的成像

在二维成像（例如 B 模）中，散射分布扩展为 $f(x,z)$ ，PSF 也变为二维的 $\text{PSF}(x,z)$ ，其形状由系统参数、换能器特性和波束形成算法共同决定。

成像过程为二维卷积：

g(x,z) = f(x,z) * \text{PSF}(x,z)

f(x,z)

：可以理解为真实反射率分布。

g(x,z)

：成像系统给出的“重建图像”（比如 DAS + 包络 + log 之后的那张 B 模图，去掉非线性就是线性的那一部分）。

\mathrm{PSF}(x,z)

：成像系统在图像域的点扩散函数（Point Spread Function）。

更准确地说，是每一个散射点都与系统对应位置的二维 PSF 进行卷积，PSF 的具体形状和大小依赖于成像系统（包括发射接收参数、换能器频率和孔径、聚焦方式、波束形成算法等）。最终图像是所有散射点响应的叠加。

在理想的空间不变系统假设下，PSF 不随位置变化，可以视作全局相同的二维卷积核。但在真实超声系统中，PSF 通常具有明显的空间变化特性，尤其在不同深度和横向位置，主瓣宽度和旁瓣结构都会变化。

实际 B 模图像中，一个组织点的成像结果就是该点与 PSF 卷积后的二维响应，其横向 FWHM 对应横向分辨率，轴向 FWHM 对应轴向分辨率。

1.1.1.3 总结

维度	真实分布	卷积核（PSF）	成像公式	含义
1D	两个点 $f(z)$	$h(z)$	$g(z)=f(z)*h(z)$	波包叠加，体现轴向分辨率
2D	平面散射 $f(x,z)$	$\text{PSF}(x,z)$	$g(x,z)=f(x,z)*\text{PSF}(x,z)$	二维 PSF，B 模图像形成

当使用仿体中的理想点散射体（近似 $\delta$ 函数）进行成像时，成像结果直接反映系统的 PSF。通过沿轴向与横向方向取剖面并测量 FWHM，即可量化系统的空间分辨率：

轴向 FWHM：由脉冲长度和带宽决定，反映轴向分辨率。
横向 FWHM：由孔径大小、聚焦方式、波束宽度决定，反映横向分辨率。

FWHM 越小，PSF 主瓣越窄，系统分辨率越高；反之则成像模糊。

超声成像系统可以近似看作一个线性空间（位移）不变系统（LSI）。真实组织的散射体分布与系统的 PSF 卷积，得到最终的超声图像。在一维、二维上，这一模型分别对应不同的卷积形式，是理解分辨率、旁瓣、去卷积、超分辨等成像技术的理论基础。

如果要求 $f$ ，那就需要对 $g$ 进行反卷积，卷积核就是PSF。

1.1.2 从数据域来看（曹章老师课的启发）

1.1.2.1 正问题和逆问题

不论什么成像系统，只要是线性系统，都可以使用 $Sx=P$ 模型来描述，其中S是系统矩阵，也叫灵敏度矩阵，在广义上可以看做一个算子，x是待测量，在超声中，即声场中的声阻抗等声学信息，P是换能器采集到的回波信号。

正问题（forward problem）
已知x和系统模型S，求 P。
也就是“给定物体和激励，预测仪器会测到什么”。

逆问题（inverse problem）
已知测量数据 P 系统模型 S，求 x。
也就是“根据仪器测到的信号，反推物体长什么样”。

因此，超声成像的仿真是一个正问题，比如使用MUST工具箱来放置散射子，然后进行RF数据回波的仿真。

而正常的超声成像是一个逆问题。

通常逆问题有三个特征：

欠定性（解可能不唯一（non-unique））
非线性
病定性（对噪声非常敏感（不稳定））

往往需要先验约束或正则化才能“好好解”。

1.1.2.2 超声中S究竟是什么

S是一个算子，但对于逆问题 $x=S^{-1}P$ 里，我们更关注的是 $S^{-1}$ ，但是由于 $S$ 有99.99%概率是病态的，也就是不可逆，或者说不满秩，甚至不是方阵，而是长条形状，所以在这里，不使用 $S^{-1}$ ，而是使用反投影（ $S^\mathrm{T}$ ）这一层近似。

让我们来推导一下：

理想情况下：

如果S是方阵、满秩，那么可以写成 $x=S^{-1}P$ ，这是严格可逆的情况下

但是成像问题中，S一般不是方阵（取决于图像矩阵维度和数据维度：RF 通道数 × 采样点数 ≠ 成像像素数），即使是方阵，也严重病态，因此逆 $S^{-1}$ 根本不存在，这里用一个方法来替代这个逆：

逆问题常用的是“最小二乘 + 正则化”，或者说是2范数+Tikhonov正则化

经典做法是：
不给你“精确方程”去解，而是解一个最小二乘：

\min_x \ \| Sx - P \|_2^2

求一阶条件的解会得到所谓“法方程（normal equations）”：

S^TSx=S^TP

此时S 的列满秩（列线性无关）的情况下， $S^TS$ 是可逆的

x=(S^TS)^{−1}S^TP

现实里通常还要做 Tikhonov正则化，因为就算“理论可逆”，数值上也很病态。加上 Tikhonov 正则化（避免不适定）：

x_{正则化后}=(S^TS+λI)^{−1}S^TP

推导结束

发现必然先出现 $S^\mathrm{T}$ ，因此，最基础的成像可以写为： $x_{B模式}=S^TP$ ，这一层叫做反投影， $S^\mathrm{T}$ 叫做反投影算子。

进行完这最基础的一步，得到的成像结果即为传统B-mode成像。

这也是为什么传统B-mode成像并不是最好的成像方法，因为仅仅做了 $x=S^TP$ ，没有做 $(S^TS+λI)^{−1}$ ，后面发展出来的各种各样的成像方法其实就是对于这个逆矩阵进行不同的变形，或者进行不同的正则化，最终得到更“像”真实的成像结果。

Sᵀ 严格说是共轭转置 Sᴴ

超声信号一般是复数（IQ 解调后更明显），严格的数学符号应该是 Sᴴ（Hermitian），这是“共轭转置 / adjoint operator”，不是单纯只对实数矩阵转置。

总结一下：

超声成像从严格意义上说是要解 $x=S^{-1}P$ 这一逆问题，但由于 S 高维、非方阵且病态，直接 $S^{-1}$ 不存在或不可用，所以实际多采用“最小二乘 + 正则化”的框架。传统 B-mode/DAS 实际只做了其中的第一步——共轭算子Sᵀ作用在数据上（反投影），即 $x_{B模式}=S^TP$ 没有显式实现 $(S^TS+λI)^{−1}$ 这一层的真正“逆运算”。

1.1.3 超声成像图像域和数据域的联系

P=Sx

是“**从物体到测量数据**”的模型，

g = f * \mathrm{PSF}

是“**从物体到重建图像**”的近似模型。

更完整地写，其实是这样一条链：

P=Sx

关键来了，其实图像 $g$ 可以看做是一个Beamforming算子 $B$ 和换能器采集回来的原始射频RF信号 $P$ 的乘积，即：

g=BP

因此：

g=BSx=Hx

若将 $BS$ 视为算子 $H$ ，那么可以将其视为整体成像算子，其直接把物体 $x$ 映射到图像 $g$ 之中。而 $x=f$ ，他们都代表着声场中声阻抗等线性信息。

所以可以写成

g=Hf

比较 $g = f * \mathrm{PSF}$ ，这样就绕回来了，其实所谓的数据域其实只是图像域重建的一部分，是包含的关系

1.2 超声成像的几种常见模式

见文章超声成像方法与波束形成Beamforming

1.3 波束形成Beamforming

见文章超声成像方法与波束形成Beamforming

1.4 超声换能器

1.4.1 压电片

1.4.1.1 压电效应

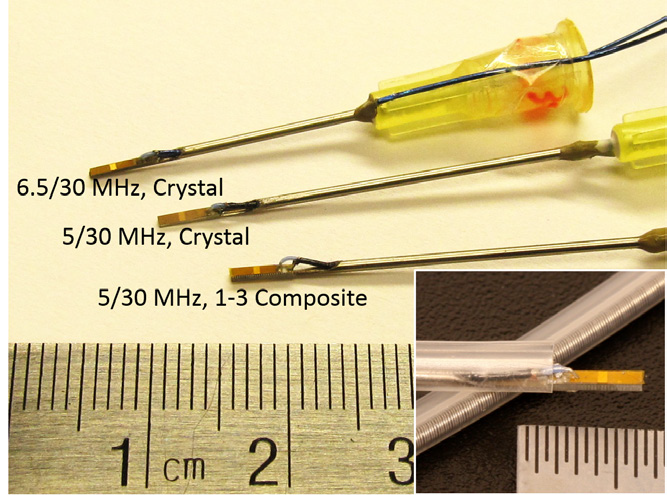
1.4.1.2 PZT 1-3 复合材料

耐压：理论值为1kV/mm，耐压值非常的高。

1.4.1.3 压电片的使用特性

例如2M/8M的双频探头，低频的激励电压是高频的4倍，能达到一致的效果

1.4.2 匹配层

1.4.3 背衬层

1.4.4 声透镜

1.4.2 不同的换能器介绍

换能器常见类型包括：线阵（Linear Array）、相控阵（Phased Array）、凸阵/曲面阵（Curvilinear Array）、环阵（Annular Array）、1.5D/2D 矩阵阵列（Matrix Array），以及为特定场景设计的腔内/血管内探头与专用型（HIFU、弹性成像、双频等）。不同类型在孔径形状、波束形成方式、视场（FOV）、可达频段与典型应用上各有侧重。

足迹 = 探头表面大小

以下是所有的类型整理：

类型	视场与足迹	频段（典型）	优势	局限	常见应用
线阵	矩形视场，足迹较宽	5–15 MHz	浅表分辨率高，几何失真小	深部穿透有限	乳腺、甲状腺、血管、肌骨
相控阵	扇形视场，足迹小	1–5 MHz	易跨肋、可快速扇扫、远场覆盖好	浅表分辨率略弱	心脏、床旁急诊、腹部
凸阵	扇形宽视野	2–6 MHz	腹部大视场、穿透力较好	近场元素稀疏，浅表一般	肝胆脾胰肾、产科
环阵	需机械/复合扫查	3–10 MHz（多样）	深度分辨率一致性好	电子偏转受限、系统复杂	专用/科研
1.5D/2D	实时 3D/4D	2–8 MHz	体数据、MPR、多角度聚焦	通道/带宽/算力要求高	3D 心超、术中/介入
腔内/IVUS	极小足迹	10–60 MHz（IVUS 可更高）	贴近靶器官、超高分辨	视野受限、操作依赖	产科/妇科、直肠、冠脉
HIFU/双频/CMUT	依用途而定	定制	声疗/高带宽/可集成	设备复杂/成本	治疗、造影、前沿研究

1.4.2.1 线阵（Linear Array）

线阵由一排线性排布的阵元构成，通常pitch会稍微大一些，

常见成像模式：动态聚焦、平面波。

特点：近场分辨率高、图像几何失真小，横向视场为矩形；探头足迹较宽。

频段/孔径：5–15 MHz（表浅/小器官可更高），孔径一般 20–50 mm。

应用：甲状腺、乳腺、肌骨、血管超声（浅表）、神经阻滞等。

1.4.2.2 相控阵（Phased Array）

相控阵同线阵一样，由一排线性排布的阵元构成，两者的区别是，相控阵的pitch通常小于 $\frac{1}{4}\lambda$ 。

相控阵通过对相位/时间延迟进行精细控制，实现电子扫描 + 电子偏转 + 电子聚焦；表面常见为小正方形或近方形孔径。

常见成像模式：动态聚焦、扇扫（Sector Scan）、合成孔径/多角度复合、平面波（高帧率）。

特点：足迹小、远场覆盖好；浅表分辨率较线阵略弱，近场孔径受限。

频段/孔径：1–5 MHz，典型孔径 15–25 mm 方口/近方口。

应用：经胸心超（TTE）、床旁急救/创伤评估（FAST）、腹部应急检查等。

1.4.2.3 凸阵/曲面阵（Curvilinear Array）

在线阵基础上做几何弯曲获得扇形视场，兼顾穿透与视野宽度，适合中深部器官。

常见成像模式：动态聚焦、扇扫、复合成像。

特点：宽视野扇扫、穿透力较好；近场元素密度相对较低，浅表成像不如高频线阵。

频段/孔径：2–6 MHz；曲率半径与有效孔径随机型而定（常见 40–70 mm 级）。

应用：腹部（肝胆脾胰肾）、产科/妇科、泌尿系统等。

1.4.2.4 环阵（Annular Array）

由同心环形阵元构成，依靠接收动态聚焦与合成孔径在各深度获得近似一致的轴向分辨率，通常配合机械扫描。

常见成像模式：机械扫查 + 动态接收聚焦、合成孔径。

特点：轴向分辨率随深度一致性好、点扩散函数对称；难以电子横向偏转，系统复杂度较高。

频段/孔径：3–10 MHz（依用途差异较大），有效孔径与环数相关。

应用：高分辨率科研成像、部分专用探头场景。

High-Frequency 64-Element Ring-Annular Array Transducer: Development ...

1.4.2.5 1.5D/2D 矩阵阵列（Matrix Array）

在一维阵列短轴方向增加多排（1.5D）或采用二维排布（2D），可在仰角/第三维实现电子聚焦与扫描，支持实时 3D/4D 成像。

常见成像模式：多平面/体数据采集、MPR、实时 3D/4D、平面波/多角度复合（高帧率）。

特点：可做体数据与多平面重建；通道数、互连与算力需求高，常配合子阵/行列寻址与多路复用。

频段/孔径：2–8 MHz 常见；2D 阵列等效通道数可达数千级，孔径依应用优化。

应用：3D/4D 心超、介入导航、术中超声以及高级产科成像等。

Figure 1 from Isfa 2012-7119 Ultrasound Transducer Array Fabrication ...

1.4.2.6 腔内与血管内探头（TEE/TV/TR/IVUS）

为贴近靶器官设计的小口径高频探头，提升信噪与分辨率。

常见成像模式：动态聚焦、机械/电子扫查；IVUS 常见机械旋转或微型阵列。

特点：极小足迹、靠近靶区、分辨率高；视野受限，对操作者要求高。

频段/孔径：

TEE（经食道）：2–7 MHz，小孔径相控阵；
腔内（经阴道/经直肠）：5–12 MHz，短焦距；
IVUS：20–60 MHz（甚至更高），微型换能器置于导管末端。

应用：TEE 心脏后壁/瓣膜评估；妇产科与直肠腔内成像；冠脉与外周血管内壁评估（IVUS）。

1.4.2.7 专用型与新型器件（HIFU/弹性/双频/CMUT/PMUT）

面向治疗、对比/谐波与超高带宽需求的定制型换能器与新材料器件。

常见成像/工作模式：

HIFU：聚焦连续/脉冲超声，声疗导航常与成像探头联用；
弹性/剪切波：推挤脉冲 + 高频跟踪，需高帧率与稳定时序；
双频/谐波：发射/接收频带分离或多带工作，增强对比与抑制散斑；
CMUT/PMUT：MEMS 工艺，宽带、可与 CMOS 集成。

特点：针对性强、带宽或声强要求高；系统集成与安全控制更复杂。

频段/孔径：依方案定制（HIFU 常为低频大孔径；双频/谐波与 MEMS 器件覆盖宽广）。

应用：无创/微创治疗、造影与对比成像、前沿器件研究与集成化超声系统。

二、非线性超声

三、论文中常见的超声概念

3.1 发射响应

概念：
发射响应用于表征换能器在接收到电信号后，将其转换为声场的能力。常用方法是给换能器施加一个脉冲或激励信号，然后使用水听器测量其发射的声压，并通过频域分析得到频率响应。

实验流程图：

flowchart LR
    A[信号发生器\n产生脉冲] --> B[功率放大器]
    B --> C[待测换能器\n发射声波]
    C --> D[水听器接收声压]
    D --> E[示波器/采集卡\n记录信号]
    E --> F[FFT 频谱分析]

3.2 接收响应

概念：
接收响应用于表征换能器作为接收器时的性能，即其将声压转换为电信号的能力。测试时需要一个参考发射换能器或已标定声源来提供已知声场，再由待测换能器接收。

实验流程图：

flowchart LR
    A[参考换能器\n发射声波] --> B(水中传播)
    B --> C[待测换能器\n接收声波]
    C --> D[前置放大器/示波器]
    D --> E[采集信号]
    E --> F[FFT 频谱分析]
    B --> G[水听器\n测量基准声压]
    G --> H["灵敏度计算 V/µPa"]
    E --> H["灵敏度计算 V/µPa"]

3.3 脉冲回波响应

概念：
脉冲回波响应是一种综合性方法，它既包含发射过程，也包含接收过程。通常做法是在水中放置一个高反射目标（如钢块），换能器发射声波后接收其回波。得到的信号既反映了发射性能，也反映了接收性能。

实验流程图：

flowchart LR
    A[信号发生器\n产生脉冲] --> B[功率放大器]
    B --> C[待测换能器\n发射声波]
    C --> D[钢块反射体]
    D --> C
    C --> E[放大器/示波器\n采集回波]
    E --> F[FFT 频谱分析]

3.4 超声图像的评价指标

3.4.1 PSF的对比度比(contrast ratio, CR)，参考jenson审稿文献

对比度使用对比度比CR衡量，基于“平均能量密度之比”。所有计算均在包络检测后的线性幅值数据上进行，不做对数压缩。计算以点扩散函数的峰值位置为中心，并定义如下感兴趣区域（regions of interest, ROIs）：

总分析窗口（Total Analysis Window / Outer Boundary）：以PSF峰值为中心的矩形区域；横向范围为±25λ，轴向范围为±10λ。
内部区域（Inside Region / Main Lobe）：以PSF峰值为中心的椭圆区域，椭圆半轴由测得的FWHM确定；横向半轴取横向FWHM的1.0倍，轴向半轴取轴向FWHM的1.0倍。
外部区域（Outside Region / Background）：位于“总分析窗口”内但在“内部椭圆”之外的所有像素。

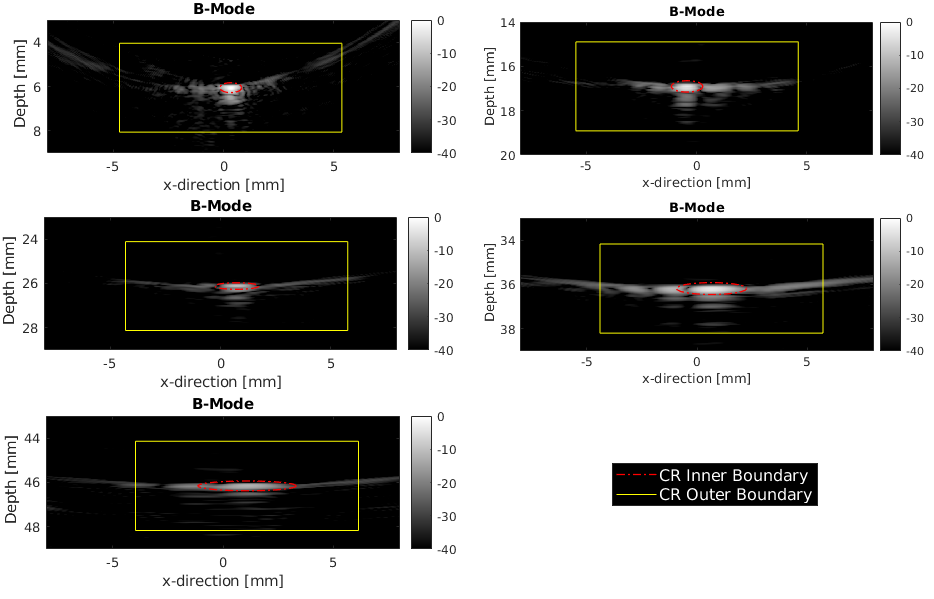
CR定义为外部区域与内部区域的“平均能量/像素”之比，并换算为dB：

CR = 20 \log_{10}\left( \sqrt{\frac{E_{\mathrm{out}}/N_{\mathrm{out}}}{E_{\mathrm{in}}/N_{\mathrm{in}}}} \right)

其中， $E_{in}$ 和 $E_{out}$ 分别为内部区域与外部区域内的总能量（包络线性幅值的平方和）； $N_{in}$ 和 $N_{out}$ 分别为内部区域与外部区域的像素数。

以上用的是线性数据：包络检测后的线性幅值（或其平方），不能在对数压缩后的B-mode灰度上直接算。

3.4.2 囊肿对比度比(contrast ratio, CR)

\mathrm{CR}=\frac{\mu_\mathrm{out}-\mu_\mathrm{in}}{\mu_\mathrm{out}+\mu_\mathrm{in}}

囊肿CR比较特殊，一般用这个CR来做，注意这个CR是Michelson contrast（米歇尔逊对比度）形式，用均值做差/和，再归一化，无单位，数值一般在 [−1,1]（常用场景下 0~1）

μ是信号滤波-包络检测-波束形成后的数值平均值（未做对数变换）

\mu_\mathrm{in}

：囊肿内部（或低回声区）的平均灰度值。<注意，这里是对于囊肿>

\mu_\mathrm{out}

：囊肿外部背景（或周围组织）的平均灰度值。

理解：

如果 $\mu_\mathrm{out}$ 远大于 $\mu_\mathrm{in}$ （亮背景 + 暗囊肿），CR 接近 1，说明对比度很高。
如果 $\mu_\mathrm{out}$ 和 $\mu_\mathrm{in}$ 差距很小，CR 接近 0，说明几乎没有对比度。
实验时会在B超图像中人工选取两块区域：inside (in)：囊肿内部或低回声目标区域。outside (out)：囊肿周围的正常背景区域。

3.4.3 对比度噪声比(contrast-to-noise ratio, CNR)

\mathrm{CNR_{dB}}=20\log_{10}\frac{\mu_{\mathrm{in}}-\mu_{\mathrm{out}}}{\sqrt{\left(\sigma_{\mathrm{in}}^{2}+\sigma_{\mathrm{out}}^{2}\right)/2}}

CNR衡量的是：在考虑图像噪声影响的前提下，囊肿与背景的对比程度。

相比CR，CNR更严格，因为它把区域内部和外部的噪声（方差）都纳入了计算。

\sigma_{\mathrm{out}}^{2}

\sigma_{\mathrm{in}}^{2}

：感兴趣区域内囊肿内外区域灰度值的方差，代表噪声水平。

3.4.4 信号与噪声比(signal-to-noise ratio, SNR)

\mathrm{SNR_{dB}}(z)=20\log_{10}\frac{\mu(z)}{\sigma(z)}

SNR 用的是同一位置（沿中心线、同一深度 z）在多帧图像上灰度值的均值与标准差。

SNR

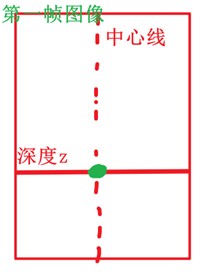
μ(z)：第 z 深度处（中心线）在100 帧上的像素（或小窗平均）的均值 → 代表“有效信号”强度。

σ(z)：同一位置、同样 100 帧上的标准差 → 代表该位置的噪声/抖动（包含电子噪声、散粒噪声等的时间波动）。

也就是说，这里的“噪声”是时间维度上的波动，不是从目标外面的一个背景 ROI 取的“空间背景标准差”。因此 σ 不是“外圈”的标准差，而是信号位置自身的标准差（跨帧/跨次采集的抖动）。

那什么时候会用“外圈背景”？CR/CNR/CTR！

SNR 则与“内/外”无关，是“同一点信号强度相对其噪声”的度量。

3.4.5 对比度组织比(contrast-to-tissue ratio, CTR)

用于造影/谐波/超谐波成像。

正规计算需要用

CTR_{dB}=20 \log_{10}\left( \sqrt{\frac{E_{\mathrm{contrast}}/N_{\mathrm{contrast}}}{E_{\mathrm{tissue}}/N_{\mathrm{tissue}}}} \right)

其中， $E_{contrast}$ 和 $E_{tissue}$ 分别为造影剂区域与组织区域内的总能量（包络线性幅值的平方和）； $N_{contrast}$ 和 $N_{tissue}$ 分别为造影剂区域与组织区域的像素数。

以上用的是线性数据：包络检测后的线性幅值（或其平方），不能在对数压缩后的B-mode灰度上直接算。

3.4.6 半峰全宽(full width at half maximum, FWHM)

3.5 f 数（f_number）

为什么要用f数：因为对于成像而言，所有的像素点都保证使用相同的f数可以提高成像质量

f_{number}=z/D

z：深度（单位：m）

D：孔径大小（单位：m）

举个例子，假设成像如果 $f_{number}=1.8$ ，对于z=30mm的像素点，此时D=16.67mm，也就是说现在需要用的孔径大小为16.67mm，如果整个换能器pitch=0.6mm，32阵元，其D_MAX=19.2mm，此时需要用的阵元数为27.78，取整为28，这样对于每个像素点都如此计算一次，最终形成一个图像像素矩阵大小（eg：2048*128）的矩阵，这个矩阵可以称为孔径矩阵，对于每个像素点，所用的阵元个数都可能不同。

五、超声仿真or计算工具

5.1 波束形成相关

5.1.1 USTB（UltraSound ToolBox）

面向“重建/波束形成与评测”的 MATLAB 工具箱，统一 UFF（自己定义的一个数据格式）数据格式，配套丰富示例与公开数据页，方便比较不同成像方法（线扫/相控阵/CPWC/STA 等），近年还加入“generalized beamformer”等先进算法实现。并非声场数值求解器，但常与 Field II、Fresnel 近似示例联动生成或读取原始通道数据。

Ultrasound Toolbox – MATLAB toolbox for processing ultrasonic signals

5.1.2 Beamformation Toolbox（Svetoslav Nikolov）

svetoslav2

用 C 语言编写的 Matlab 工具箱，用于超声数据的波束形成。它支持标准波束形成方法以及合成孔径聚焦。支持多种聚焦类型：固定聚焦、多重聚焦、动态聚焦和基于像素的聚焦。偏重重建，不做声场求解。

Beamformation Toolbox | Svetoslav Nikolov

5.2 声场计算相关

5.2.1 Field II（Jørgen Jensen）

最广泛使用的超声模拟工具。它基于Tupholme–Stepanishen/空间脉冲响应（SIR）的概念，能高效生成各类换能器/序列的回波通道数据与脉冲/连续波场，广泛用于点扩散函数、阵列设计与“可控的模拟数据”生产。线性声学近似；非线性传播需借助其他工具。

Field II Ultrasound Simulation Program

5.2.2 k-Wave（Bradley Treeby, Ben Cox, Jiri Jaros）

kwave

基于 k 空间伪谱法的 MATLAB 和 C++开源声学工具箱。该软件专为在复杂和仿真的组织中进行的时域声学和超声模拟而设计。可模拟非线性、频率依赖衰减、强异质介质中的波传播；提供超声成像/束形相关示例（如发射束形、波束图），但定位是声场数值求解器而非专职波束形成框架。

k-Wave: A MATLAB toolbox for the time domain simulation of acoustic wave fields

5.2.3 The DREAM Toolbox（Fredrik Lingvall）

开源的 SIR/阵列建模 工具箱，侧重常见与复杂阵列形状的空间脉冲响应计算，可做**波束转向/聚焦/加权（apodization）**分析，适合阵列设计、近/远场脉冲响应评估，支持近场和远场的宽带脉冲激励。不自带完整的重建流水线或公开数据集。

The DREAM Toolbox

5.2.4 FOCUS（Robert J. McGough）

FOCUS 是一款跨平台超声仿真工具，基于快速近场法和角谱方法，用于计算单个换能器和相控阵列产生的压力场。

FOCUS | Michigan State University

5.3 工具对比

工具	是否开源波束形成	支持的典型波束形成	是否提供开源数据集	是否提供声场计算	声场计算思路/差异
USTB	是（DAS/DRF、CPWC/STA 等；含 generalized beamformer）	线扫/相控阵定焦、平面波/多角合成、STA 等（示例丰富）	有数据页（统一 UFF，含仿真/体模/体内等入口）	有限（示例/对接 Field II/Fresnel；自身非场解算器）	主要做“数据→重建/评测”；声场多由 Field II 等外部生成。
Beamformation Toolbox（Nikolov）	是（强调“标准方法”与合成孔径，C 加速）	传统 DAS、动态聚焦、像素级聚焦、单/双/多态合成孔径	无（聚焦算法工具，不含数据仓库）	否	不做 PDE/场仿真，专注高速重建。
Field II	间接（可生成通道并示例简单成像，但核心是仿真）	可配合实现线扫/相控阵/STA（依赖用户脚本）	无数据仓库（但可“仿真生成”任意场景数据）	是	基于 SIR（T-S 方法）的线性声学近似；高效、适合系统级与点扩散函数分析。
k-Wave	否（示例有束形/波束图，但非重建框架）	—（可输出场或虚拟通道后自写重建）	无	是	时域伪谱法直接数值求解波动方程，支持非线性/频率依赖衰减/强异质；计算更重，但物理更全面。
DREAM	否（更像阵列/SIR 计算与分析）	—（可做聚焦/转向/加权分析）	无	是	SIR 计算多几何阵列（含脉冲宽带），便于阵列形状与加权研究；不产重建流水线。
FOCUS	否（定位为压力场快速计算）	—	无	是	快速压力场（单元/阵列、HIFU 友好），MATLAB 接口丰富；侧重稳态/脉冲场的高效计算与工程参数扫描。