超声多普勒成像原理及诊断技术

[^1]: 超声原理及生物医学工程应用 | WorldCat.org

一、超声多普勒原理

1.1 普适性的多普勒频移

多普勒频移有三个对象，分别是：1.观测者；2.声源；3.介质（空气、水…）

分别对这三者的运动进行对公式的补充，最终生成一个3D空间笛卡尔坐标下的超声多普勒定律。

1.1.1 设定

• 声速（相对介质本身）：$c$
• 介质均匀定常流（沿 (+x)）：$U$
• 声源固有发射频率：$f_0=\frac{1}{T_0},\ \omega_0=2\pi f_0$
• 声源速度（沿 (+x)）：$V_s$（朝观测者为正）
• 观测者速度（沿 (+x)）：$V_o$（向波传播方向为正）

要找：观测者位置处测到的频率 $f_{\text{obs}}$。

---

1.1.2 全部静止：$U=0,\ V_s=0,\ V_o=0$

观测点处场量（位移/压力/粒子速度）都是以 $f_0$ 做简谐振动，因此

$$f_{\text{obs}}=f_0$$

---

1.1.3 加介质运动：$U\neq 0,\ V_s=0,\ V_o=0$

介质均匀定常流会改变波长（波数），但不会改变“时间单频强迫”的频率。观测点仍看到同一频率振动：

$$f_{\text{obs}}=f_0$$

---

1.1.4 加声源运动：$U\neq 0,\ V_s\neq 0,\ V_o=0$

在地面坐标中，波峰的前进速度为

$$c+U$$

相邻两次发射间隔为 $T_0$，声源在这段时间前进 $V_sT_0$，因此前方波列波长为

$$\lambda=(c+U)T_0 - V_sT_0=(c+U-V_s)T_0$$

观测者固定时，观测频率 =（波峰通过速度）/（波长）：

$$f_{\text{obs}}=\frac{c+U}{\lambda} = f_0\frac{c+U}{c+U-V_s}$$

---

1.1.5 加观测者运动：$U\neq 0,\ V_s\neq 0,\ V_o\neq 0$

观测者也在运动时，波峰相对观测者的接近速度为

$$(c+U)-V_o$$

波长仍由声源运动决定：

$$\lambda=(c+U-V_s)T_0$$

所以最终观测频率：

$$f_{\text{obs}} =\frac{(c+U)-V_o}{\lambda} =f_0\frac{c+U-V_o}{c+U-V_s}$$

---

1.1.6 3D 矢量形式

令 $\hat{\mathbf{n}}$ 为声从声源指向观测者的传播方向单位向量，把速度取沿传播方向的分量：

$$U_n=\mathbf{U}\cdot\hat{\mathbf{n}},\quad V_{s,n}=\mathbf{V}*s\cdot\hat{\mathbf{n}},\quad V*{o,n}=\mathbf{V}_o\cdot\hat{\mathbf{n}}$$

则

$$f_{\text{obs}}= f_0* \frac{c+U_n-V_{o,n}} {c+U_n-V_{s,n}} = f_0* \frac{c+\mathbf{U}\cdot\hat{\mathbf{n}}-\mathbf{V}_o\cdot\hat{\mathbf{n}}} {c+\mathbf{U}\cdot\hat{\mathbf{n}}-\mathbf{V}_s\cdot\hat{\mathbf{n}}}$$

1.2 医学中的超声多普勒原理简化

由于在超声成像中，超声波发射和接收都是固定住的超声换能器，对于整个发射与接收过程来说，其是一个对称的两次多普勒频移过程，即从换能器→声场中血管的血流，发生了第一次多普勒频移，换能器是声源，血流是观测者。从血管的血流→换能器，发生了第二次多普勒频移，血流是声源，换能器是观测者。

由上可知，超声成像中的多普勒过程可以分解为两个连续的一次多普勒频移过程。

一次多普勒频移发生在超声换能器向血流传播的过程中。此时，换能器作为声源，血流作为观测者。设换能器发射的超声中心频率为 ( $f_0$)，血流速度为 ( v )，声束与血流方向夹角为 ( $\theta$ )，介质中的声速为 ( c )，则血流处接收到的频率为：

$$f_1 = f_0 \frac{c + v \cos\theta}{c}$$

血流中的散射体（如红细胞）对超声波进行散射，并将其回传至换能器。在回传过程中，血流相当于声源，换能器作为观测者，发生第二次多普勒频移。此时换能器接收到的回波频率为：

$$f_2 = f_1 \frac{c}{c - v \cos\theta}$$

将一次多普勒频移的结果代入，可得：

$$f_2 = f_0 \frac{c + v \cos\theta}{c - v \cos\theta}$$

医学超声多普勒中关注的是回波信号频率相对于发射频率的变化量，即多普勒频移量，定义为：

$$\Delta f = f_2 - f_0$$

在血流速度远小于声速（v << c）的条件下，对上述表达式进行一阶近似，可得医学超声中常用的多普勒频移公式：

$$\Delta f = \frac{2 f_0 v \cos\theta}{c}$$

最终要求的是血流$v$

$$v=\frac{c}{2}\cdot\frac{\Delta f}{f}\cdot\frac{1}{cos\theta}$$

二、超声多普勒信号的解调方式

解调分为非定向解调和定向解调：

2.1 非定向解调

非定向解调就是只求多普勒效应的大小，不管方向，也就是无法生成红蓝颜色的血流方向。

2.1.1 相干解调

相干解调就是1 相乘 2 滤波。

由于多普勒频移 $f_D$ 相比超声发射频率 $f_0$ 很小，工程上通常采用相干解调的方法：将接收回波与发射参考信号相乘，通过产生差频分量来提取多普勒信息。对于静止组织回波，其频率与发射信号一致，相位关系固定，相乘后仅形成直流分量；而运动散射体产生的频移信号在相干解调后会保留下低频调制项，从而实现多普勒频移检测。

设发射超声作为参考信号，其幅值归一化、初相位取零：

$$E(t)=\cos(\omega_0 t)$$

由运动目标产生的频移回波可表示为：

$$R_D(t)=B\cos(\omega_0 t+\omega_D t+\varphi_D)$$

同时，来自静止组织的杂波分量写为：

$$R_0(t)=A\cos(\omega_0 t+\varphi_0)$$

其中 $A,B$ 分别为杂波与多普勒信号幅度，$\varphi_0,\varphi_D$ 为相对于参考信号的初相位。多普勒角频率满足：

$$\omega_D=\frac{2v}{c}\omega_0$$

这里 $v$ 为目标轴向速度，$c$ 为声速。

接收总回波可表示为两者叠加：

$$R(t)=A\cos(\omega_0 t+\varphi_0)+B\cos(\omega_0 t+\omega_D t+\varphi_D)$$

相干解调通过将回波与参考信号相乘：

$$D(t)=R(t)\cdot E(t)$$

代入后得到：

$$D(t)=[A\cos(\omega_0 t+\varphi_0)+B\cos(\omega_0 t+\omega_D t+\varphi_D)]\cos(\omega_0 t)$$

展开并利用积化和差公式，可整理为：

$$D(t)=\frac{A}{2}[\cos(2\omega_0 t+\varphi_0)+\cos\varphi_0] +\frac{B}{2}[\cos(2\omega_0 t+\omega_D t+\varphi_D)+\cos(\omega_D t+\varphi_D)]$$

可以看到，解调结果包含两类分量：

• 以 $2\omega_0$ 为中心的高频项
• 位于基带附近的低频项

通过低通滤波去除高频分量 $2\omega_0$ 后，保留下来的信号为：

$$D_L(t)=\frac{A}{2}\cos\varphi_0+\frac{B}{2}\cos(\omega_D t+\varphi_D)$$

其中第一项为与时间无关的直流分量，对应静止杂波；第二项为多普勒频移分量，包含运动目标的速度信息。

需要注意的是，该相干解调过程仅保留了 $\omega_D$ 的幅值信息，而无法区分其正负号，因此不能直接判断血流方向。这种解调方式属于非定向解调，后续需结合正交解调或相域处理才能实现方向判别。

2.1.2 非相干解调

非相干解调不需要入射波信号，并使用同态滤波技术来滤除载波频段信号。

2.1.2.1 解调流程

设系统发射参考信号（未知）为

$$R_0(t)=Acos(w_0t)$$

其中 $\omega_0$ 为发射角频率，$A$ 为静态组织回波幅度。

当存在运动散射体（如血流）时，接收回波可表示为

$$R(t)=Acos(\omega_0 t)+Bcos(\omega_0 t+\omega_D t+\varphi_D)$$

其中：

• $B$ 为血流回波幅度，通常满足 $A\gg B$；
• $\omega_D$ 为多普勒角频率；
• $\varphi_D$ 为相对于发射波的相位。

对第二项展开：

$$R(t)=Acos(\omega_0 t)+Bcos(\omega_0 t)cos(\omega_D t+\varphi_D)-Bsin(\omega_0 t)sin(\omega_D t+\varphi_D)$$

整理：

$$R(t)=Xcos(\omega_0 t)+Ysin(\omega_0 t)$$

其中：

$$X=A+Bcos(\omega_D t+\varphi_D) \\ Y=-Bsin(\omega_D t+\varphi_D)$$

整理：

$$R(t)=\sqrt{(X^2+Y^2)}\,sin(\omega_0 t+\varphi)$$

由于血流回波幅度远小于背景回波$A\gg B$，有：

$$\sqrt{X^2+Y^2}=\sqrt{A^2+2ABcos(\omega_D t+\varphi_D)+B^2}$$ $$\sqrt{X^2+Y^2}\approx A+Bcos(\omega_D t+\varphi_D)$$

于是回波信号可写成：

$$R(t)=[A+Bcos(\omega_D t+\varphi_D)]\,sin(\omega_0 t+\varphi)$$

下一步就是考虑如何滤除回波信号中的$\omega_0$部分，保留$\omega_D$部分，这里可以使用同态滤波技术（利用$\omega_0$大，$\omega_D$小）。

2.1.2.2 同态滤波技术

这一节既是例子又是技术的总结，同态滤波通常用来去除乘性噪声。

上一节中回波信号写成：

$$R(t)=[A+Bcos(\omega_D t+\varphi_D)]\,sin(\omega_0 t+\varphi)$$

上述表达式属于典型的乘性模型：

$$R(t)=m(t)\cdot c(t)$$

其中：

$$m(t)=A+Bcos(\omega_D t+\varphi_D)\\ c(t)=sin(\omega_0 t+\varphi)$$

传统线性滤波难以直接分离乘性成分，因此引入同态变换，下面就是同态变换的过程：

1. 对数变换：乘法变加法

   $$\ln R(t)=\ln m(t)+\ln c(t)$$

   此时：

   • $\ln c(t)$主要集中在高频（载波）
   • $\ln m(t)$主要分布于低频（多普勒调制）

   乘法关系被转化为加法关系，实现频域可分离。

2. 频域滤波：傅里叶变换+滤波器
   对 $ln R(t)$进行傅里叶变换：

   $$Y(\omega)=\mathcal{F}\{\ln R(t)\}$$

   构造高通或带阻滤波器 $H(\omega)$，抑制载波对应频段，仅保留调制分量：

   $$\tilde{Y}(\omega)=H(\omega)Y(\omega)$$

   再经反变换：

   $$\tilde{y}(t)=\mathcal{F}^{-1}\{\tilde{Y}(\omega)\}$$

3. 指数恢复：

   $$\tilde{m}(t)=\exp(\tilde{y}(t))$$

   得到：

   $$\tilde{m}(t)\approx A+Bcos(\omega_D t+\varphi_D)$$

   至此完成载波抑制，多普勒调制信号被成功提取。

该过程等价于：对数压缩动态范围 → 将调幅转为加性结构 → 频域滤除载波 → 指数恢复包络。在连续多普勒和脉冲多普勒超声系统中，该方法常用于血流速度估计、微弱频移提取以及组织背景抑制，属于经典的非相干解调实现路径。

2.2 定向解调

定向解调相比于非定向解调，就是多了一个方向问题，这个方向是通过对$\omega_0$进行比较来获得，大于$\omega_0$就是顺流信号，用F表示，小于$\omega_0$就是逆流信号，用R表示。

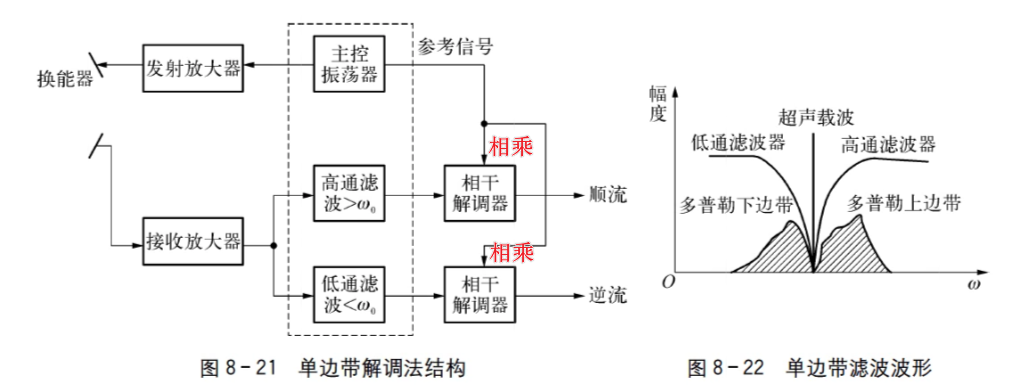
2.2.1 单边带解调法

可将接收换能器接收的频移信号表示为：

$$R_D(t)=A_F cos(\omega_0 t+\omega_F t)+A_R cos(\omega_0 t-\omega_R t)$$

式中，$A_F,\omega_F$ 为顺流信号的振幅和多普勒频移，$A_R,\omega_R$为逆流信号的振幅和多普勒频移。

在实际解调时，利用精密调谐的射频滤波器，在频移信号中将多普勒上、下边带 $(\omega_0+\omega_F)$、$(\omega_0-\omega_R)$ 分离。这需要采用一个高通和一个低通滤波器完成，分别让超声回波先放大后再经多普勒上、下边带通过。随后，上、下边带在独立通道中进行相干解调，从而分别获得顺向和逆向的多普勒频移信号，同时得到血流的流速与方向信息。

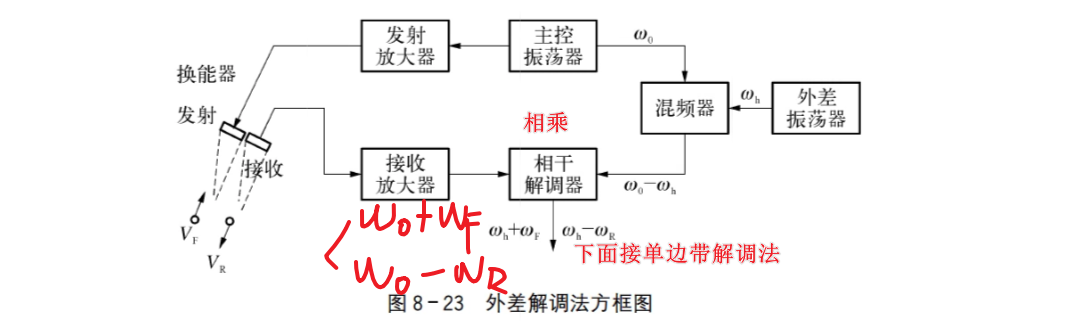
2.2.2 外差解调法

主振荡器产生的高频信号 $\omega_0$ 不直接作为相干解调器的参考信号，而是先与外差振荡器产生的信号 $\omega_h$ 进入混频器，产生差频信号 $(\omega_0-\omega_h)$ 作为参考信号。然后再与包含方向信息的回波信号进行相干解调，使输出包含 $(\omega_h+\omega_F)$ 和 $(\omega_h-\omega_R)$ 的分量，从而获得速度和方向双重信息。该方法可用于“连续波式”和“脉冲波式”多普勒诊断仪器。

在“连续波”式工作方式时，设含有杂波、顺流和逆流分量的回波信号 $R(t)$ 表示为：

$$R(t)=A\cos(\omega_0 t+\varphi_0)+B_F\cos(\omega_0 t+\omega_F t+\varphi_F)+\\B_R\cos(\omega_0 t-\omega_R t+\varphi_R)$$

混频输出的外差信号（相干解调器的参考信号）可表示为：

$$H(t)=\cos(\omega_0 t-\omega_h t)$$

相干解调中，两信号相乘，根据积化和差公式 $\cos\alpha\cos\beta=[\cos(\alpha+\beta)+\cos(\alpha-\beta)]/2$ 可得：

$$\begin{aligned} D(t)=\frac{1}{2}\{& A\cos(2\omega_0 t-\omega_h t+\varphi_0) +B_F\cos(2\omega_0 t+\omega_F t-\omega_h t+\varphi_F) \\ &+B_R\cos(2\omega_0 t-\omega_R t-\omega_h t+\varphi_R) +A\cos(\omega_h t+\varphi_0) \\ &+B_F\cos(\omega_h t+\omega_F t+\varphi_F) +B_R\cos(\omega_h t-\omega_R t+\varphi_R) \} \end{aligned}$$

由低通滤波滤除高频分量 $2\omega_0$ 后得：

$$D_F(t)=\frac{1}{2}\Big[A\cos(\omega_h t+\varphi_0)+B_F\cos(\omega_h t+\omega_F t+\varphi_F)+\\B_R\cos(\omega_h t-\omega_R t+\varphi_R)\Big]$$

然后再利用单边带滤波方法分离出正向流和逆向流，最后用相干解调求出正向流和负向流多普勒频移的大小。

2.2.3 正交相位解调法

该方法的基本思想是：先检测多普勒频移信号的实部和虚部，然后再加以处理，从而获得流向信息。该方法效果较好，在定向型多普勒诊断仪中使用较多，可工作于连续波式或脉冲波式。

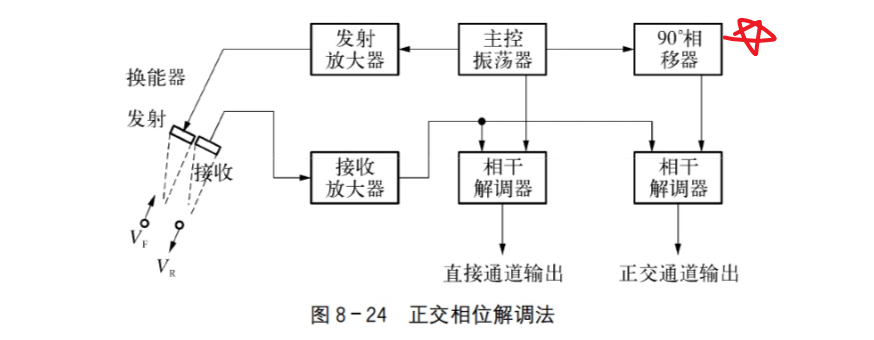
具体做法是：将回波信号经放大后分两路进入两路相干解调器。一路解调器的参考信号取自主控振荡器，称为直接通道；另一路参考信号取自主控振荡器经 $90^\circ$ 移相后的信号，称为正交通道。两参考信号频率相同，相位相差 $90^\circ$。

设接收信号为 $R(t)$（包含杂波、顺流和逆流分量），用参考信号 $\cos(\omega_0 t)$ 与 $R(t)$ 相干解调，并滤去 $2\omega_0$ 的高频部分，得到直接通道输出 $D(t)$ 为：

$$D(t)=\frac{1}{2}A\cos\varphi_0+\frac{1}{2}B_F\cos(\omega_F t+\varphi_F)+\frac{1}{2}B_R\cos(\omega_R t-\varphi_R)$$

这里D就是同相分量I 实部

正交通道参考信号为 $\cos(\omega_0 t-90^\circ)=\sin(\omega_0 t)$，与接收信号相干解调并滤除高频信号，得到正交通道输出 $Q(t)$ 为：

$$Q(t)=-\frac{1}{2}A\sin\varphi_0-\frac{1}{2}B_F\sin(\omega_F t+\varphi_F)+\frac{1}{2}B_R\sin(\omega_R t-\varphi_R)$$

这里Q就是正交分量Q 虚部

再将静止目标的杂波信号滤除，可得：

$$D(t)=\frac{1}{2}B_F\cos(\omega_F t+\varphi_F)+\frac{1}{2}B_R\cos(\omega_R t-\varphi_R)$$ $$Q(t)=\frac{1}{2}B_F\cos(\omega_F t+\varphi_F+90^\circ)+\frac{1}{2}B_R\cos(\omega_R t-\varphi_R-90^\circ)$$

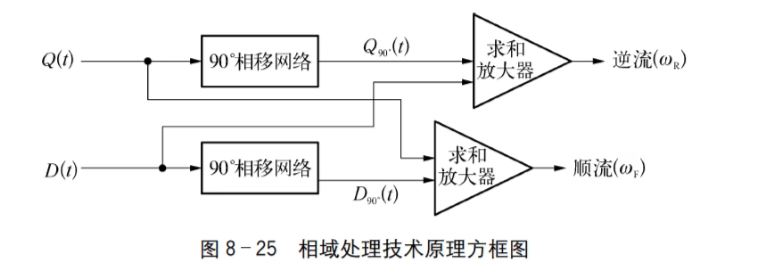
直接通道与正交通道输出都包含顺流和逆流的信息，还需经相域（见图8-25）或频域处理才能分离方向信息。将正交通道输出的 $Q(t)$ 信号超前 $90^\circ$，再与 $D(t)$ 求和后得到逆流信号为：

$$B_R\cos(\omega_R t-\varphi_R)$$

同理，将直接通道的输出 $D(t)$ 信号超前 $90^\circ$，再与 $Q(t)$ 求和后得到顺流信号（利用 $\cos(\pi/2+\alpha)=-\sin\alpha$）为：

$$-B_F\sin(\omega_F t+\varphi_F)$$

这样，就得到了正向流和负向流的多普勒频移信息。相域处理技术原理如图8-25所示。

以上所有内容我都自己推导完毕，没有问题。