超声成像方法与波束形成Beamforming

一、超声成像方法

超声成像方法指的是：发射端的方法

1.1 传统方法

1.1.1 电子延迟线扫成像

只要一次发射，经过波束形成后，图像中生成的都是一条线（也就是扫描线，或者说是一个一维向量），那就都是线扫

通过施加电子延迟，实现线扫，

有没有焦点：有，虽然是线扫，但是也要发射聚焦到一个深度点上

1.1.2 电子延迟扇扫成像

只要一次发射，经过波束形成后，图像中生成的都是一条线（也就是扫描线，或者说是一个一维向量），那就都是线扫

1.2 新型方法

1.2.1 合成孔径成像SA

合成孔径成像启发于雷达的合成孔径，传统合成孔径成像可以参考jensen2006年的综述：Synthetic aperture ultrasound imaging - ScienceDirect

其使用一个一个阵元分别激励，使用全孔径接收，比如128阵元，就会产生128帧RF数据，之后在经过波束形成进行成像。

通过单个阵元激励合成孔径成像效果还是提升很大的

1.2.1.1 虚拟点源

虚拟点源是为了提升超声换能器的成像孔径而提出的一种方法。

其工作原理示意图：

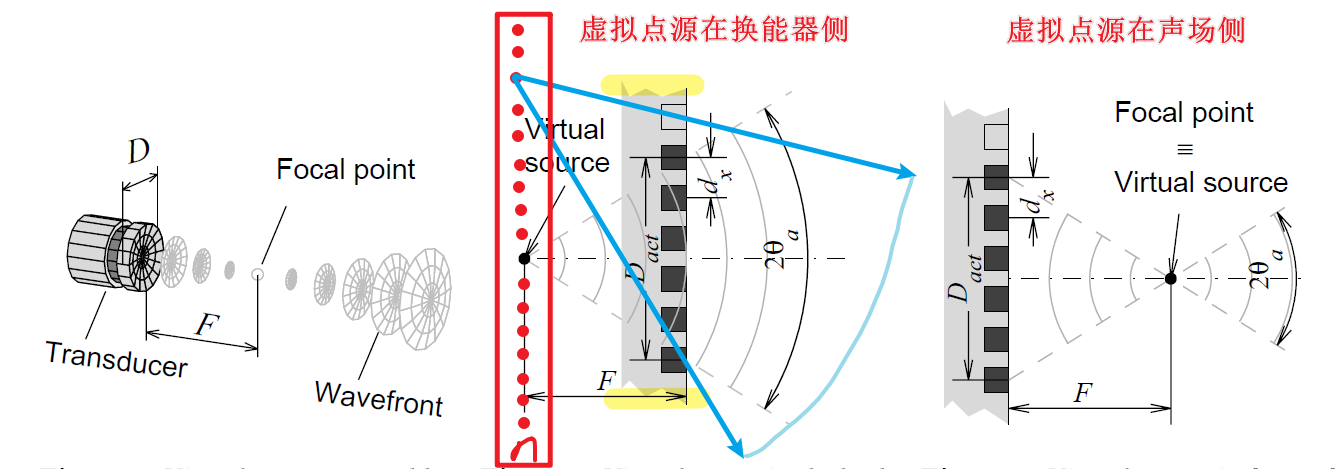
换能器阵列通过施加电子延迟，产生在换能器前或后的一个个虚拟点源。红色的一个个的点即为虚拟点源，可以将他们视为发出超声波的声源，而换能器阵列变成了声波路径上的一些途经点，变得没有意义，可以忽略他们的存在，之后在计算任何delay的时候，只需要考虑这一帧是这一个红色的点源发出的声波即可。

观察虚拟点源在换能器侧示意图，可以看到，本来换能器孔径只有比较小的范围，但是通过虚拟点源方法，相当于扩展了其孔径，理论上其孔径可以扩展的无限大，孔径在一定范围内增大可以大幅提高成像的横向分辨率。如下图所示：

1.2.1.2 虚拟点源在换能器侧

如上上图所示，当虚拟点源在换能器侧时，其就相当于在换能器侧有一个点源发出声波，而不是换能器阵元面发射，后面所有的波束形成等方法都以这个点源作为发射端即可。

1.2.1.3 虚拟点源在声场侧

如上上图所示，当虚拟点源在声场侧时（其实就是相当于使用电子延迟使波束聚焦在声场中一个点上，类似动态聚焦聚焦波），其就相当于在声场侧有一个点源发出声波，而不是换能器阵元面发射，那么这个声波是要先返回换能器面吗？不是的，要强调一下虚拟点源这个概念，在发射时，他就是探头，因此，我们要把他作为一个点源换能器，发射的声波直接向下面的声场传播，发射延迟因此也要改变。

但是接收延迟还是声场中的散射点距离换能器阵元的距离。

1.2.1.4 合成孔径成像提速：滑动窗口相干合成

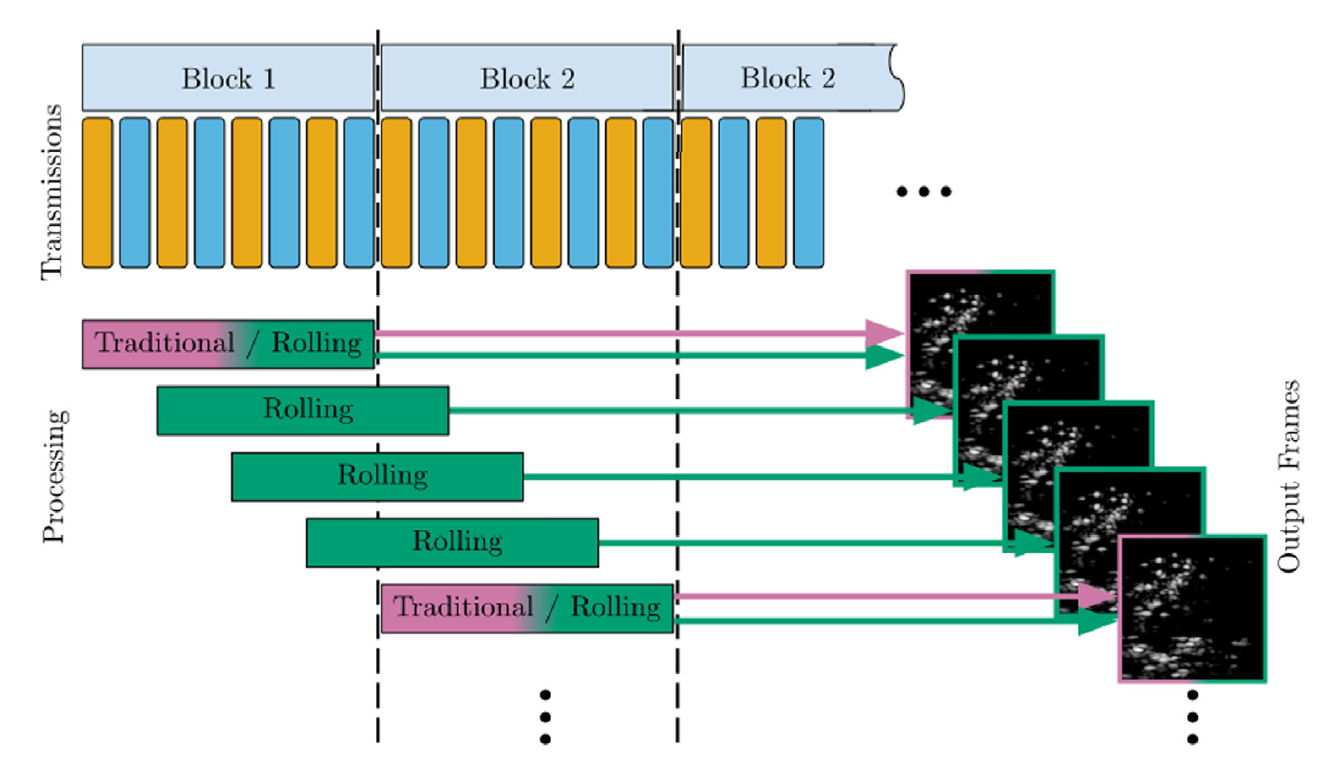
1.2.2 平面波成像

平面波成像在原理上可以视为一种特殊的合成孔径成像

1.2.2.1 单角度平面波成像

1.2.2.2 多角度平面波相干复合成像

1.2.3 TO法横向震动法

二、波束形成方法

2.1 什么是波束形成

波束形成和以上提出的超声成像方法有些杂糅，不好区分，这里我们做下规定：

波束形成不包含滤波、取包络、插值、对数变换、加窗、变迹
波束形成不包含超声发射方法
这里说的波束形成只谈对采集回来的信号进行不同的处理，以实现类延迟叠加的效果

下面正式开始：

黑箱理论：一个RF数据被采集回来后，经过一个黑箱，产生图像，被人眼所接收。

那么这个黑箱就格外重要，黑箱里面有什么？

有数据裁剪、滤波、取包络、波束形成、图像滤波、图像去噪、图像锐化、卷积、神经网络识别、大模型分割…….

也就是说，对于一个确定的RF数据（原始数据真实性由传感器决定），后面的黑箱，才是成像是否真、是否有意义的real决定性因素。

其中波束形成也是这里面可操作性最强之一的流程。

波束形成来源于自适应天线，接收端的信号处理，可以通过对多天线阵元接收到的各路信号进行加权合成，形成所需的理想信号。

超声中波束形成的定义为：通过数字延时补偿替代传统模拟延时线实现精确信号控制，其关键技术包括动态聚焦、动态孔径调整和幅度变迹，支持逐点跟踪式信号处理。该技术突破模拟系统的通道数限制，显著提升成像分辨率与稳定性。

插一嘴，md加矩阵的规定：

2.2 为什么要用波束形成

2.3 DAS(delay-and-sum)

2.3.1 DAS整体流程

DAS即delay-and-sum顾名思义为先延迟再相加，那么对象是谁？没错，对象就是我们通过AD采集回来的RF射频数据，这个射频数据应该有C列，分别对应C个探头；有R行，分别对应采样深度R，即为采样点个数为R。

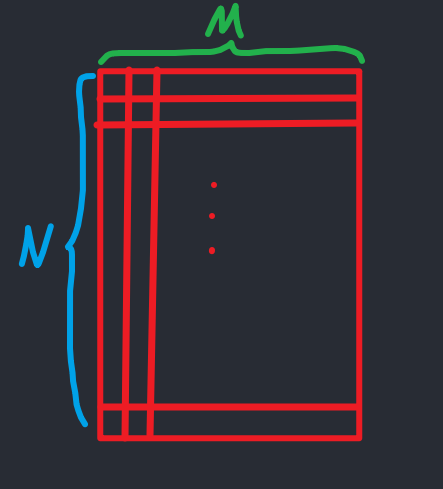
delay_size

先不考虑图像的插值问题，假设图像矩阵大小与射频矩阵大小一致。DAS的整体流程为：

graph TD
 A[换能器信息]-->|构造|C[M*N个延迟阵 每个延迟阵都对应一个image像素点];
 B[目标image: I 矩阵 像素数长M宽N信息]-->|构造|C;
 C-->D[根据其中1个延迟阵取T中的RF数据并相加];
 E[T 矩阵 RF数据矩阵]-->D;
 D-->F[得到 I 矩阵中其中一个aij数据]

反复重复以上操作，重复M*N次之后，完整的image矩阵就做出来了，使用这个图像矩阵就可以直接显示了，也可以基于此在做各类的算法进行图像优化。

2.3.2 DAS数学推导

也就是说：

RF矩阵 $T$ 大小为 $R*C$
延迟阵 $D$ 大小为 $M*N$
图像阵 $I$ 大小为 $M*N$
如上所述，先默认认为 $M=R,N=C$ ，也就是构建的图像矩阵大小与射频矩阵大小相同

现在每个像素点对应一个延迟阵，成像域一共有 $M*N$ 个像素点，因此一共有 $M*N$ 个延迟阵D，为 $D_{ij}$ ， $i\in M,j\in N$ ，其中image中的第 $ij$ 个像素点数值为：

\begin{matrix} a_{ij}=\langle D_{ij},T\rangle_F=\sum_{m=1}^M\sum_{n=1}^N D_{ij}(m,n)T(m,n)=\mathrm{tr}\left(D_{ij}^\top T\right) \end{matrix}

\mathrm{I}= \begin{pmatrix} \mathrm{a}_{11} & \mathrm{a}_{12} & ... & \mathrm{a}_{1N} \\ \mathrm{a}_{21} & \mathrm{a}_{22} & ... & \mathrm{a}_{2N} \\ ... & ... & ... & ... \\ \mathrm{a}_{M1} & \mathrm{a}_{M2} & ... & \mathrm{a}_{MN} \end{pmatrix}

其中 $\langle D_{ij},T\rangle_F$ 为矩阵内积。注意如果RF数据为 $128*2048$ ，图像想要 $1000 * 5000$ ，上面公式中的T就不能用m,n了，需要使用r,c来替代。

好的，目前，回顾一下，我们已经知道怎么求图像阵了，也有RF射频矩阵，目前不知道的只有 $D$ 延迟阵了，下面来求延迟阵：

我们之前已经假设了图像和换能器的行列数相同，那意味着图像列数与换能器阵元个数相同，图像行数与depth采样深度相同。

这里取 $X_i$ 为换能器阵列的x横坐标， $\Delta t$ 为1个单位depth的延迟时间。

\mathrm{D}= \begin{pmatrix} \mathrm{d}_{11} & \mathrm{d}_{12} & ... & \mathrm{d}_{1N} \\ \mathrm{d}_{21} & \mathrm{d}_{22} & ... & \mathrm{d}_{2N} \\ ... & ... & ... & ... \\ \mathrm{d}_{M1} & \mathrm{d}_{M2} & ... & \mathrm{d}_{MN} \end{pmatrix}

D矩阵计算步骤：

求点到各换能器阵元的距离
距离/c——>转换成延迟
通过延迟/ $\Delta t$ 求出格点的位置，并令这个位置的 $d_{ij}$ 为1
完成D矩阵的构造

到此为止，一个完整的DAS流程就实现了，可以出图喽。